这也算是矩阵运算的一个应用吧,顺便学用一下SDL,哈哈!
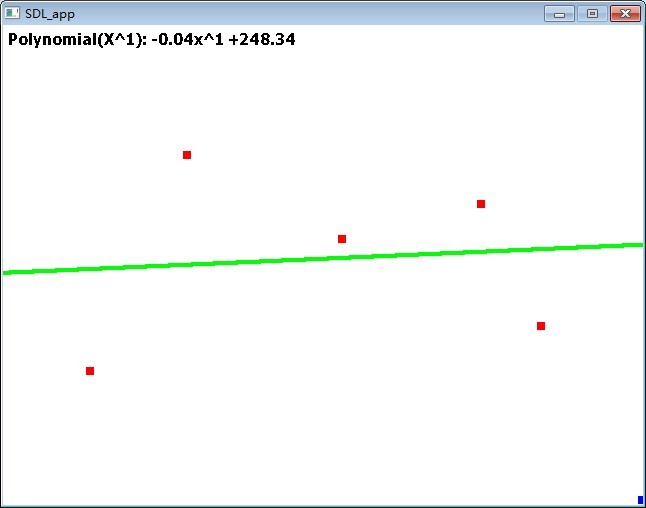
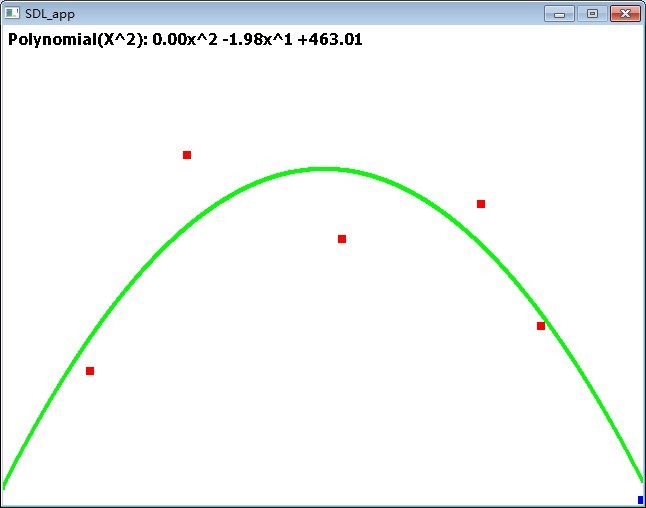
给出5个离散点,分别选用不同的多项式来拟合一条曲线:
这是最常见的最小二乘法得到的直线方程:
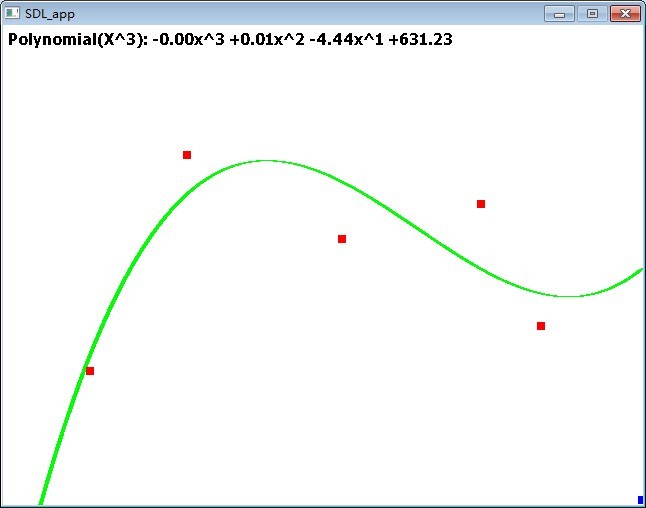
拟合三次曲线:
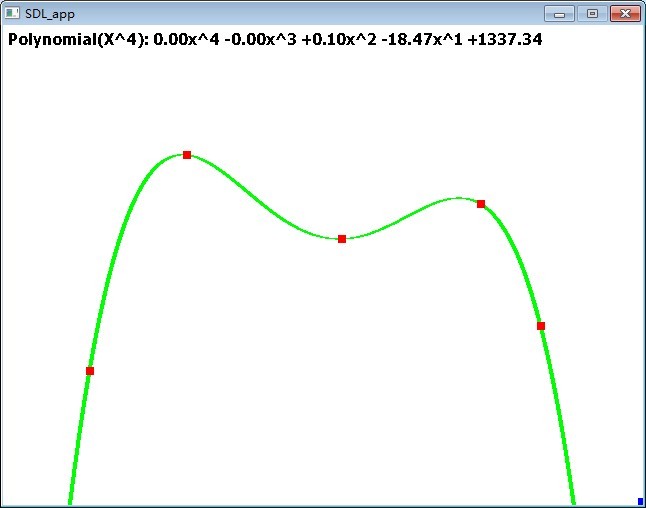
四次曲线:
综合上述各种情况,很容易发现的规律是使用的多项式次数越高,虽然离散点的拟合效果很好,但是曲线的波动越大,不一定实用。
下面再举一个数据例子说明这个问题:
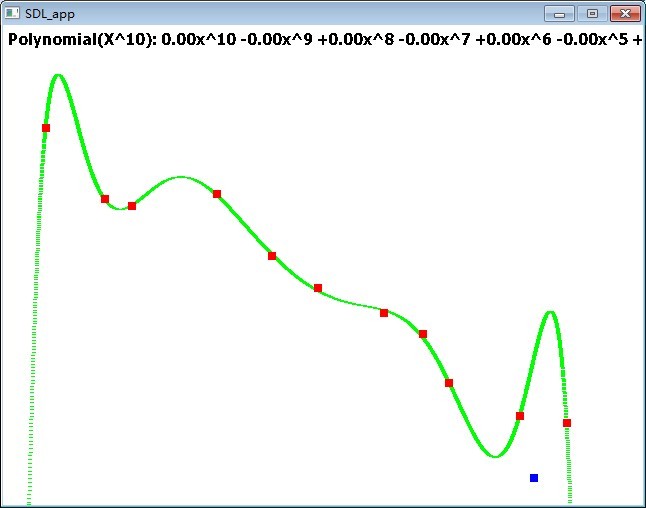
当多项式越复杂时,
当最高次项的指数为5时,拟合效果比上面的可能要好,相对而然比较稳定。
花了一天时间来写矩阵运算和多项式的生成,也值得了,对Numerical Methods这门课程算是有了深入的理解。
哈哈,花了很长时间不断地找错,后来发现我的程序计算错误的原因是我把乘号两边的矩阵变量位置搞反了。修正这个错误后,立马得到了正确答案,兴奋不已,拍案叫绝!
我坚信,实践总是比背书效果要好的!

恩,实践总是比背书效果要好的!
小虾也用 c++ 哈哈~
提个小建议: operator *, / 这种对称的运算符不要作为成员函数,否则 matrix_a * matrix_b 会变成 matrix_a.operator *(matrix_b),于是 a 不能隐式构造而 b 却可以,造成不对称~
何为对称运算符?求教! 是a*b,b*a这样的交换律?
就是说 a 和 b 具有一样的性质
比如如果把 + 声明为 std::string 的成员,s 是一个实例,那么
s + “abc” 是合法的,而 “abc” + s 是非法的
如果声明到类外,二者都是合法的
如此来说,STL string的+重载是声明在类内的啊!
如果我声明在类外,是不是可以解决问题了?
据说 STL 的 std::string 就是声明在类外的
不过后者效率还是会低一些,Imperfect C++ 嘛
………………………………
我头晕……
晕?!找虾哥帮你人工呼吸,,,
哥上个月实习的时候,人工呼吸最后一次测试12个全部达标,拿了惊人的100分
不错,学习啊
好深奥
看来我们读文科的真的不适合这些啊,好复杂,头都晕了
我也很头痛!!!
我系实用派,那些什么定理虽然自己不一定能理解,不一定能证明,但系我懂得怎么用就够啦!
嗯, 头痛, 不过受教了.
貌似在matrix67的博客中看到过,说多项式逼近复杂度越大,越抖动
嗯!matrix67牛!
自信please。